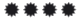\([T,L^2]=[H,L^2]=[L^2,L_i]=[H,L_z]=0\)
La respuesta no habla de L^2, sino de L
En un sistema cualquiera no sabemos lo que da el conmutador [E,L], hay que hallarlo, entonces en un sistema aislado L es constante y el hamiltoniano del sistema es la energía que también se conserva y al hallar el conmutador se nos va a hacer cero, (acordaros que en los operadores cuánticos siempre hay derivadas) luego el truco esta en "sistema aislado".
Ea, no tiene nada que ver el que la componente z de L conmute con la energía para que también lo haga L, de hecho lo normal es E y L no conmuten, es más, lo que conmuta con L_z es el hamiltoniano y este no siempre es la energía del sistema
O al menos, esto es lo que tengo entendido