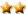A=Axi+Ayj. Su módulo será: \(A^2=Ax^2+Ay^2\)
B=Bxi+Ayj. Su módulo será: \(B^2=Bx^2+By^2\)
Entonces, trabajando con los módulos:
\(\frac{A}{B}=\frac{(Ax^2+Ay^2)^(\frac{1}{2})}{(Bx^2+By^2)^(\frac{1}{2})}=\frac{Ax}{Bx}\) La última igualdad es lo que te pide el enunciado.
Entonces:
\(\frac{Ax^2}{Bx^2+By^2}+\frac{Ay^2}{Bx^2+By^2}=\frac{Ax^2}{Bx^2}\)
\(Ax^2+Ay^2=\frac{Ax^2 * (Bx^2+By^2)}{Bx^2}\)
\(Ax^2+Ay^2=Ax^2 + \frac{Ax^2*By^2}{Bx^2}\)
Entonces, para que se cumpla la igualdad:
\(Ay^2=\frac{Ax^2+By^2}{Bx^2}\)
Por lo que:
\(\frac{Ay^2}{Ax^2}= \frac{By^2}{Bx^2}\)
Y quitando los cuadrados:
\(\frac{Ay}{Ax}= \frac{By}{Bx}\)
Una cosa, en la 193decís que la velocidad inicial de la pelota C es la que mayor velocidad tiene en el eje y, pero yo no lo acabo de ver. ¿que me lo podríais explicar? Yo y mis problemas de primero de carrera...
Gracias!!!
Bueno, voy a seguir corrigiendo... es que son interminables mis correcciones!!!
Por cierto, ¿ya os habéis inscrito?