Impugnaciones
Moderador: Alberto
Impugnaciones
Hola a todos ¿Qué tal lo lleváis?
Estaba viendo que por aquí no hay movimiento pero sí muchas plantillas introducidas y que en gaia tampoco es que se maten por hablar como otros años. De hecho sólo hay colgadas 2 impugnaciones (16 y 165) y apenas unas pocas preguntas debatidas.
La cuestión es ¿pasáis de impugnar? ¿estáis en otro foro que no conozco? Veo que en el foro de gaia también se extrañan, lo pregunto por aquí porque es más visible
Estaba viendo que por aquí no hay movimiento pero sí muchas plantillas introducidas y que en gaia tampoco es que se maten por hablar como otros años. De hecho sólo hay colgadas 2 impugnaciones (16 y 165) y apenas unas pocas preguntas debatidas.
La cuestión es ¿pasáis de impugnar? ¿estáis en otro foro que no conozco? Veo que en el foro de gaia también se extrañan, lo pregunto por aquí porque es más visible
Re: Impugnaciones
Buenas !!
Yo me pongo hoy con ello por que hasta ahora no había metido la plantilla.
En gaia no me aceptan el usuario, asi que si pudieras ponerlas por aquí las que dices que han pasado sería
Y si tienes alguna propuesta más pues encantado de compartirlas. Ya te digo que esta tarde me pongo con ello.
¿Que tal os fue a los que estuvisteis activos por aqui (rakel jeusus... )?
Yo me pongo hoy con ello por que hasta ahora no había metido la plantilla.
En gaia no me aceptan el usuario, asi que si pudieras ponerlas por aquí las que dices que han pasado sería
Y si tienes alguna propuesta más pues encantado de compartirlas. Ya te digo que esta tarde me pongo con ello.
¿Que tal os fue a los que estuvisteis activos por aqui (rakel jeusus... )?
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
Rakel, yo he enviado por mi cuenta impugnaciones de las preguntas 75, 78 y 142.
Re: Impugnaciones
Aquí tenéis las subidas a gaia.
- Adjuntos
-
- Anulación, 165 (1).pdf
- (146.69 KiB) Descargado 346 veces
-
- 165 cambio.pdf
- (231.02 KiB) Descargado 331 veces
-
- 16 cambio de respuesta.pdf
- (104.1 KiB) Descargado 353 veces
Re: Impugnaciones
¿Y qué impugnas? La 75 y la 142 diría que están bien (lo digo por debatir, no por prohibir, que conste). La 78 ni idea.antonio-rf escribió: ↑03 Feb 2022, 15:12 Rakel, yo he enviado por mi cuenta impugnaciones de las preguntas 75, 78 y 142.
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
Te paso las impugnaciones. No sé si es el formato adecuado para hacerlasRakel escribió: ↑03 Feb 2022, 15:34¿Y qué impugnas? La 75 y la 142 diría que están bien (lo digo por debatir, no por prohibir, que conste). La 78 ni idea.antonio-rf escribió: ↑03 Feb 2022, 15:12 Rakel, yo he enviado por mi cuenta impugnaciones de las preguntas 75, 78 y 142.
75.
La función de onda del átomo de hidrógeno se puede expresar según [1]
φ(r) = R(r) Ylm (θ, φ),
con Ylm(θ, φ) el armónico esférico que contiene toda la dependencia angular. Todo armónico esférico se puede expresar según [2]
Ylm (θ, φ) ∝ Plm(cos θ) e^{imφ},
con e^{imφ} una fase compleja y Plm(x) las funciones ASOCIADAS de Legendre, distintas de las funciones de Legendre.
[1]. Cohen-Tannoudji, C., Diu, B., Laloë, F. "Mécanique Quantique", Nouvelle édition, EDP Sciences/CNRS Éditions. Tome I, section A-2-a, equation A-20.
[2]. Weisstein, Eric W. "Spherical Harmonic." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/SphericalHarmonic.html
78.
Sea G el grupo de simetrías del sistema de interés y sea H el subgrupo de simetrías no rotas H. El número de modos Nambu-Goldstone es igual al número de generadores de simetría rotos o, equivalentemente, a la dimensión del espacio cociente G/H [1,2], [3],
n_{NM} = n_{BG} = dim(G/H) = dim G - dim H.
Nuestro grupo de simetrías original es H = O(3), y el grupo de simetrías rotas es G = O(2). O(n) tiene un generador por cada dimensión [1,2]. Por tanto, el número de modos Nambu-Golstone son 3-2 = 1 modo, no 2. De igual manera, dim O(3) = 3 y dim O(2) = 2, luego dim(G) - dim(H) = 1.
[1] Watanabe, H. "Counting Rules of Nambu-Goldstone Modes", Annu. Rev. Condens. Matter Phys. 2020. 11:1–15.
[2] Beekman, A. J., Rademaker, L., van Wezel, J., "An introduction to spontaneous symmetry breaking", SciPost Phys. Lect. Notes 11 (2019).
[3]. John M. Lee, "Introduction to Smooth Manifolds", Second Edition, theorem 21.17.
142.
El decaimiento α siempre involucra un descenso en 4 unidades del número másico A y en 2 unidades el número atómico Z [1], luego el núcleo resultante con respecto al núcleo padre no puede ser ni isótopo, ni isómero, ni isótono ni isóbaro.
[1]. Krane, K. S., 1988. "Introductory Nuclear Physics". John Wi- ley & Sons. Capı́tulo 8.
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
No estoy de acuerdo con la 16, creo que es correcta. Como dice la bibliografía que habéis usado, la fuerza de rozamiento se opone al movimiento relativo entre sólidos en el punto de contacto. Consideremos dos casos: rodadura con y sin deslizamiento, en ambos casos con velocidad angular cuyo vector vemos salir hacia nosotros (regla del sacacorchos), es decir, gira como giran las ruedas de los coches habitualmente.
Si se rueda con deslizamiento, entonces la velocidad en el punto de contacto es no nula. De hecho, la dirección del movimiento en tal punto irá en sentido contrario al movimiento del CM. Como el CM va hacia arriba, esta velocidad va hacia abajo.
Si rueda sin deslizamiento, entonces la velocidad del punto de contacto es nula. La fricción que debe aparecer para oponerse a tal movimiento debe tener dirección contraria al movimiento en el punto de contacto, es decir, debe ir hacia arriba, a lo largo de la dirección de movimiento del coche, que es la dirección de movimiento del CM. Por tanto, podemos descartar todas menos la tres. El valor numérico es como habéis calculado, mg sinα. Con mi explicación anterior se podría entender vuestro resultado aparentemente paradójico.
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
Acabo de darme cuenta de mi fallo en la 142  . Es isótopo por las dos betas!
. Es isótopo por las dos betas!
Re: Impugnaciones
Exactamente te iba a decir eso en la 142.
Al impugnar puedes pedir anulación y cambio de respuesta
Sobre la 16, lo que venimos a decir es que igual que en la bibliografía cuando el aro cae, que matemáticamente la fuerza de rozamiento va en contra del movimiento, cuando el coche sube, también será así. Entonces al bajar el aro si que hay una fuerza peso que baja y una fuerza de rozamiento que sube. Si el coche bajara sería lo mismo. Pero al subir el coche, tienes dos fuerzas que bajan y ninguna que sube por lo que ¿como narices haces que se anule para que sea v constante? La única forma es llevarte la contraria con la disposición de las fuerzas y sería un absurdo.
Al impugnar puedes pedir anulación y cambio de respuesta
Sobre la 16, lo que venimos a decir es que igual que en la bibliografía cuando el aro cae, que matemáticamente la fuerza de rozamiento va en contra del movimiento, cuando el coche sube, también será así. Entonces al bajar el aro si que hay una fuerza peso que baja y una fuerza de rozamiento que sube. Si el coche bajara sería lo mismo. Pero al subir el coche, tienes dos fuerzas que bajan y ninguna que sube por lo que ¿como narices haces que se anule para que sea v constante? La única forma es llevarte la contraria con la disposición de las fuerzas y sería un absurdo.
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
Gracias, pediré cambio de respuesta en la 78.
Sobre la 16 he encontrado esto: http://laplace.us.es/wiki/index.php/Sis ... a_aplicada, donde destacan este texto y esta imagen: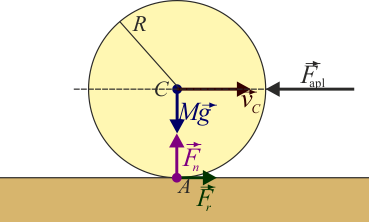
La demostración sirve para cualquier fuerza constante, por tanto la conclusión es igualmente válida para la gravedad. Es un resultado bastante poco intuitivo la verdad, pero no sé cuándo vi el resultado en algún lado y se me quedó por lo paradójico que es.
Sobre la 16 he encontrado esto: http://laplace.us.es/wiki/index.php/Sis ... a_aplicada, donde destacan este texto y esta imagen:
Observemos que la fuerza, al ser de rozamiento estático, se opone a la fuerza aplicada. Por tanto, en el caso de una rueda que avanza sometida a un rozamiento con el aire, la fuerza de rozamiento con el suelo va hacia adelante, es decir, en el mismo sentido que la velocidad del centro de la rueda. Para explicar como es que en este caso el rozamiento parece favorecer el movimiento, en vez de oponerse a él, hay que recordar que en el punto contacto la velocidad es nula, por lo que la fuerza aplicada tiende a desplazar este punto en su propio sentido, y la fuerza de rozamiento a lo que se opone es a este desplazamiento del punto de contacto, no al del CM.

La demostración sirve para cualquier fuerza constante, por tanto la conclusión es igualmente válida para la gravedad. Es un resultado bastante poco intuitivo la verdad, pero no sé cuándo vi el resultado en algún lado y se me quedó por lo paradójico que es.
Re: Impugnaciones
Pero fíjate que ahí la fuerza de rozamiento va en contra d ela fuerza aplicada. Va a favor de la rodadura como dije en la impugnacion, pero en contra de la fuerza aplicada y como dices, la gravedad es una fuerza aplicada.
El problema es ese. Se han querido pasar de listos con el lenguaje y no se han dado cuenta de que matemáticamente es imposible. Si el coche bajara estaría perfecto, tendríamos dos fuerzas contrarias y podríamos decir que la fuerza de rozamiento va a favor de las ruedas. Pero no baja, sube.
El problema es ese. Se han querido pasar de listos con el lenguaje y no se han dado cuenta de que matemáticamente es imposible. Si el coche bajara estaría perfecto, tendríamos dos fuerzas contrarias y podríamos decir que la fuerza de rozamiento va a favor de las ruedas. Pero no baja, sube.
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
La respuesta del examen dice que "1703.5 N en el sentido del movimiento.", y efectivamente, como se ve en la imagen y como se demuestra matemáticamente en la página, la fuerza de rozamiento va según el movimiento, es decir, en la imagen va paralela a vc y contraria a Faplicada, que es la gravedad. Creo que está bien la respuesta. Si algo hay que criticar es querer preguntar algo tan específico 
Re: Impugnaciones
Pero para llegar al resultado correcto, al igual que en la imagen tuya y en la de la impugnacion( que es de un libro) va en sentido contrario.
Pero bueno. Podríamos discutir eternamente me parece. Enseguida subo más impugnaciones
Pero bueno. Podríamos discutir eternamente me parece. Enseguida subo más impugnaciones
- antonio-rf
- H
- Mensajes: 7
- Registrado: 30 Ene 2022, 18:36
Re: Impugnaciones
Rakel, como dices la fuerza va en sentido contrario a la fuerza aplicada, pero es que no te preguntan por eso (!). Te piden la dirección no con respecto a la fuerza aplicada sino con el movimiento. Efectivamente, la fuerza va en el mismo sentido que el movimiento si va se mueve cuesta arriba (nuestro caso) y contraria al sentido del movimiento si se mueve cuesta abajo (el caso de tu pdf). En la demostración de la página de la US consideran ambos casos, y más arriba también el caso cuando no hay fuerza externa.
Re: Impugnaciones
Envío impugnaciones
- Adjuntos
-
- 081.pdf
- (307.88 KiB) Descargado 343 veces
-
- 102-anulación.pdf
- (133.56 KiB) Descargado 331 veces