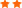Dudas estado sólido
Moderador: Alberto
Dudas estado sólido
Abro este hilo para preguntar un par de cuestiones que no soy capaz de llegar al resultado.
1.- Supongamos que existe un solo electrón libre en una caja unidimensional de 0,1 nm. ¿Cuál es la energía de Fermi?
a) 8,2 eV
b) 13,6 eV
c) 1,5 ·10^-20 J
d) 1,5 ·10^-18 eV
e) 9,4 eV
Lo que hago es lo siguiente: \(E_{F}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{N}{V}]^{2/3}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{1}{(0,1\cdot10^{-9})^3}]^{2/3}\)....y no llego a nada!!!
2.- La densidad numérica de los electrones en el cobre es 8,47 e/nm^3. ¿Cuál es su energía de Fermi a T=0K?
a) 7eV
b) 9,4 eV
c) 13,6 eV
d) 1,12 ·10^-18 eV
e) 1,5 ·10^-18 J
Aplico la misma formula de antes: \(E_{F}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{N}{V}]^{2/3}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{8,47}{(0,1\cdot10^{-9})^3}]^{2/3}=1,51 eV\)
3.- Un conductor de cobre de densidad 8,8g/cm^3 tiene una sección de 1mm^2 y por él circula una corriente de 4A.Calcular la velocidad de arrastre de los electrones a su través (masa atómica del cobre 63,57g/mol)
a) 2·10^-4 m/s
b) 10^-4 m/s
c) 3·10^-4 m/s
d) 2,5·10^-4 m/s
e) 1,5·10^-4 m/s
Aqui aplico \(v=\frac{I}{nqS}\)
\(n=8,8\frac{g}{cm^3}\cdot \frac{1mol}{63,57g}\cdot \frac{N_{Av}}{1mol}\cdot \frac{10^6cm^3}{1m^3}=8,336455\cdot 10^{28}at/m^3\)
\(v=\frac{I}{nqS}=\frac{4}{8,336455\cdot 10^{28}\cdot 1,602\cdot 10^{-19}\cdot 10{-6}}=2,995\cdot 10^{-4}m/s\)
Con lo que me sale la respuesta 3....os da lo mismo???
Gracias!!
1.- Supongamos que existe un solo electrón libre en una caja unidimensional de 0,1 nm. ¿Cuál es la energía de Fermi?
a) 8,2 eV
b) 13,6 eV
c) 1,5 ·10^-20 J
d) 1,5 ·10^-18 eV
e) 9,4 eV
Lo que hago es lo siguiente: \(E_{F}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{N}{V}]^{2/3}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{1}{(0,1\cdot10^{-9})^3}]^{2/3}\)....y no llego a nada!!!
2.- La densidad numérica de los electrones en el cobre es 8,47 e/nm^3. ¿Cuál es su energía de Fermi a T=0K?
a) 7eV
b) 9,4 eV
c) 13,6 eV
d) 1,12 ·10^-18 eV
e) 1,5 ·10^-18 J
Aplico la misma formula de antes: \(E_{F}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{N}{V}]^{2/3}=\frac{h^2}{8m_{e}}[\frac{3}{\pi}\frac{8,47}{(0,1\cdot10^{-9})^3}]^{2/3}=1,51 eV\)
3.- Un conductor de cobre de densidad 8,8g/cm^3 tiene una sección de 1mm^2 y por él circula una corriente de 4A.Calcular la velocidad de arrastre de los electrones a su través (masa atómica del cobre 63,57g/mol)
a) 2·10^-4 m/s
b) 10^-4 m/s
c) 3·10^-4 m/s
d) 2,5·10^-4 m/s
e) 1,5·10^-4 m/s
Aqui aplico \(v=\frac{I}{nqS}\)
\(n=8,8\frac{g}{cm^3}\cdot \frac{1mol}{63,57g}\cdot \frac{N_{Av}}{1mol}\cdot \frac{10^6cm^3}{1m^3}=8,336455\cdot 10^{28}at/m^3\)
\(v=\frac{I}{nqS}=\frac{4}{8,336455\cdot 10^{28}\cdot 1,602\cdot 10^{-19}\cdot 10{-6}}=2,995\cdot 10^{-4}m/s\)
Con lo que me sale la respuesta 3....os da lo mismo???
Gracias!!
Re: Dudas estado sólido
La primera pregunta es una caja UNIDIMENSIONAL y por eso no vale la formula que estas aplicando ya que eso es para 3 dimensiones aun asi a mi no me da los 9,4 eV me da 4 veces mas
la formula seria Ef=(h*Kf)^2/(((2*PI)^2)*2*m)
Kf=PI/a
donde Ef=Energia de Fermi y Kf=el vector de onda de fermi
yo creo que a hacer la cuenta han puesto la mitad del tamaño del pozo
Las otras dos preguntas me salen lo mismo que a ti y no se donde esta el error
siento escribir asi las formulas pero no tengo latex en este ordenador
la formula seria Ef=(h*Kf)^2/(((2*PI)^2)*2*m)
Kf=PI/a
donde Ef=Energia de Fermi y Kf=el vector de onda de fermi
yo creo que a hacer la cuenta han puesto la mitad del tamaño del pozo
Las otras dos preguntas me salen lo mismo que a ti y no se donde esta el error
siento escribir asi las formulas pero no tengo latex en este ordenador
Re: Dudas estado sólido
Muchas gracias!!
Re: Dudas estado sólido
Añado alguna mas que este tema.... 


1.- El niobio pasa al estado superconductor al ser enfriado por debajo de 9K. Si el campo crítico para la superconductividad es 0,1T calcular la corriente máxima que puede transportar un cable de niobio de 2 mm de diámetro para permanecer en estado superconductor en ausencia de campos externos.
a) 5mA
b) 50mA
c) 5A
d) 50A
e) 500A
2.- La separación internuclear para la molécula de NaCl es 0,236nm. Los datos espectrales muestran que la curvatura K del potencial es 109J/m^2. El potencial de ionización del sodio es 5,2 eV y la afinidad electrónica del cloro es 3,65 eV. Con estos parámetros, determinar el parámetro \(\alpha\) de la expresión del potencial iónico.
a) 1.235eV
b) 1.893eV
c) 2.725eV
d) 3.173 eV
e) 4.642eV
3.- El óxido de calcio cristaliza en un red tipo NaCl, donde la arista de la celda unidad mide 4,81\(\AA\). Calcular la densidad del óxido de calcio.
a) 3.34 g/cc
b) 2.26 g/cc
c) 1.89 g/cc
d) 5.63 g/cc
e) 4.32 g/cc
Gracias!!
1.- El niobio pasa al estado superconductor al ser enfriado por debajo de 9K. Si el campo crítico para la superconductividad es 0,1T calcular la corriente máxima que puede transportar un cable de niobio de 2 mm de diámetro para permanecer en estado superconductor en ausencia de campos externos.
a) 5mA
b) 50mA
c) 5A
d) 50A
e) 500A
2.- La separación internuclear para la molécula de NaCl es 0,236nm. Los datos espectrales muestran que la curvatura K del potencial es 109J/m^2. El potencial de ionización del sodio es 5,2 eV y la afinidad electrónica del cloro es 3,65 eV. Con estos parámetros, determinar el parámetro \(\alpha\) de la expresión del potencial iónico.
a) 1.235eV
b) 1.893eV
c) 2.725eV
d) 3.173 eV
e) 4.642eV
3.- El óxido de calcio cristaliza en un red tipo NaCl, donde la arista de la celda unidad mide 4,81\(\AA\). Calcular la densidad del óxido de calcio.
a) 3.34 g/cc
b) 2.26 g/cc
c) 1.89 g/cc
d) 5.63 g/cc
e) 4.32 g/cc
Gracias!!
- Usuario0410
- Rn

- Mensajes: 876
- Registrado: 23 Sep 2013, 09:48
Re: Dudas estado sólido
Respondo a la 3. Primero mira la imagen adjunta de la celda unidad:
Entonces:
-O bien te coges la celda unidad entera de arista 4.81 A.
-O haces los cálculos para uno de los ocho cuadrantes cada uno de arista (4.81/2) A. Hago este último método:
\(\rho(g/cc)=\frac{\lef(\frac{1}{8}4(40g)+\frac{1}{8}4(16g)\right)/N_{avo}}{\frac{4.81}{2}\times 10^{-24}}= 3.3424 g/cc\)
Las otras dos, ni idea.
Entonces:
-O bien te coges la celda unidad entera de arista 4.81 A.
-O haces los cálculos para uno de los ocho cuadrantes cada uno de arista (4.81/2) A. Hago este último método:
\(\rho(g/cc)=\frac{\lef(\frac{1}{8}4(40g)+\frac{1}{8}4(16g)\right)/N_{avo}}{\frac{4.81}{2}\times 10^{-24}}= 3.3424 g/cc\)
Las otras dos, ni idea.
- Adjuntos
-
- salpuntos.jpg (11.24 KiB) Visto 19091 veces
Re: Dudas estado sólido
Usuario0410 escribió:Respondo a la 3. Primero mira la imagen adjunta de la celda unidad:
Entonces:
-O bien te coges la celda unidad entera de arista 4.81 A.
-O haces los cálculos para uno de los ocho cuadrantes cada uno de arista (4.81/2) A. Hago este último método:
\(\rho(g/cc)=\frac{\lef(\frac{1}{8}4(40g)+\frac{1}{8}4(16g)\right)/N_{avo}}{\frac{4.81}{2}\times 10^{-24}}= 3.3424 g/cc\)
Las otras dos, ni idea.
Muchas gracias....la verdad es que soy negada para solido....jejeje
Re: Dudas estado sólido
Añado un par de dudas mas:
1.- La densidad de átomos para cierta red de estructura cubica simple es \(3\cdot10^{-22}cm^{-3}\). La constante de red de la estructura será:
a)6,85A
b) 1,46A
c) 1,03nm
d) 3,22A
e) 0,86nm
2.- Si la constante de red del silicio vale 5,43A calcular la distancia entre el centro de un átomo de silicio y el centro de su vecino más próximo.
a)1,18A
b) 3,41A
c) 2,36A
d) 5,43A
e) 6,18A
3.- Se mide la distancia de equilibrio y la energía de disociación de la molécula LiF, obteniendose los valores de 1564A y 5,99 eV. Determinar el potencial V(R) suponiendo que dicho potencial viene dado como \(V(R)=A(e^{-2a(R-R_{0})}-2e^{-a(R-R_{0})})\), donde \(R_{0}\) es la distancia de equilibrio y A=6,05 eV
a)3,76eV
b) 5,89eV
c) -6,05eV
d) -3,76eV
e) 4,46eV
4.- Considerad la molécula de \(He_{2}\) caracterizada por las constante a=1,56A y b=5,6·10^{-22}J en el potencial de Lennard-Jones. Calcular la energía del punto cero en la aproximación de oscilador armónico.
a) \(1,82\cdot10^{-3}eV\)
b) \(2,82\cdot10^{-3}eV\) RC
c) \(3,82\cdot10^{-3}eV\)
d) \(4,82\cdot10^{-3}eV\)
e) \(5,82\cdot10^{-3}eV\)
Muchas gracias!!!
1.- La densidad de átomos para cierta red de estructura cubica simple es \(3\cdot10^{-22}cm^{-3}\). La constante de red de la estructura será:
a)6,85A
b) 1,46A
c) 1,03nm
d) 3,22A
e) 0,86nm
2.- Si la constante de red del silicio vale 5,43A calcular la distancia entre el centro de un átomo de silicio y el centro de su vecino más próximo.
a)1,18A
b) 3,41A
c) 2,36A
d) 5,43A
e) 6,18A
3.- Se mide la distancia de equilibrio y la energía de disociación de la molécula LiF, obteniendose los valores de 1564A y 5,99 eV. Determinar el potencial V(R) suponiendo que dicho potencial viene dado como \(V(R)=A(e^{-2a(R-R_{0})}-2e^{-a(R-R_{0})})\), donde \(R_{0}\) es la distancia de equilibrio y A=6,05 eV
a)3,76eV
b) 5,89eV
c) -6,05eV
d) -3,76eV
e) 4,46eV
4.- Considerad la molécula de \(He_{2}\) caracterizada por las constante a=1,56A y b=5,6·10^{-22}J en el potencial de Lennard-Jones. Calcular la energía del punto cero en la aproximación de oscilador armónico.
a) \(1,82\cdot10^{-3}eV\)
b) \(2,82\cdot10^{-3}eV\) RC
c) \(3,82\cdot10^{-3}eV\)
d) \(4,82\cdot10^{-3}eV\)
e) \(5,82\cdot10^{-3}eV\)
Muchas gracias!!!
Re: Dudas estado sólido
soiyo escribió:Añado un par de dudas mas:
1.- La densidad de átomos para cierta red de estructura cubica simple es \(3\cdot10^{-22}cm^{-3}\). La constante de red de la estructura será:
a)6,85A
b) 1,46A
c) 1,03nm
d) 3,22A
e) 0,86nm
yo creo que el enunciado esta mal ya que 3e-22 at en un cm3 me parecen muy pocas yo creo que eso seria vacio o ultra alto vacio pero si consideramos 3e22 at cm3 entonces como la celda cubica simple solo tiene un atomo por celda tendriamos \(\sqrt[3]{\frac{1}{3E22}}=3.21E-8cm=3.21A\)
2.- Si la constante de red del silicio vale 5,43A calcular la distancia entre el centro de un átomo de silicio y el centro de su vecino más próximo.
a)1,18A
b) 3,41A
c) 2,36A
d) 5,43A
e) 6,18A
El silisio al igual que el carbono tiene la estructura tretragonal famosa que con carbono es la del diamante pero hay 4 celdas en la celda unidad mira el enlace para ver el dibujo http://solarsur.8m.com/Celda.htm
la diagonal de un cubo es \(d=a\sqrt{3}\) y como la distacia es la 4 parte de la diagonal
\(r=\frac{a\sqrt{3}}{4}=\frac{5.43\sqrt{3}}{4}=2.31\)
Re: Dudas estado sólido
alain_r_r escribió:soiyo escribió:Añado un par de dudas mas:
1.- La densidad de átomos para cierta red de estructura cubica simple es \(3\cdot10^{-22}cm^{-3}\). La constante de red de la estructura será:
a)6,85A
b) 1,46A
c) 1,03nm
d) 3,22A
e) 0,86nm
yo creo que el enunciado esta mal ya que 3e-22 at en un cm3 me parecen muy pocas yo creo que eso seria vacio o ultra alto vacio pero si consideramos 3e22 at cm3 entonces como la celda cubica simple solo tiene un atomo por celda tendriamos \(\sqrt[3]{\frac{1}{3E22}}=3.21E-8cm=3.21A\)
Se me colo el signo negativo al escribir...muchas gracias!!!!
2.- Si la constante de red del silicio vale 5,43A calcular la distancia entre el centro de un átomo de silicio y el centro de su vecino más próximo.
a)1,18A
b) 3,41A
c) 2,36A
d) 5,43A
e) 6,18A
El silisio al igual que el carbono tiene la estructura tretragonal famosa que con carbono es la del diamante pero hay 4 celdas en la celda unidad mira el enlace para ver el dibujo http://solarsur.8m.com/Celda.htm
la diagonal de un cubo es \(d=a\sqrt{3}\) y como la distacia es la 4 parte de la diagonal
\(r=\frac{a\sqrt{3}}{4}=\frac{5.43\sqrt{3}}{4}=2.31\)
Gracias!!!! bufff...cuanto conseguire saber hacer estos ejercicios!!!


Re: Dudas estado sólido
Una mas para este sufrimiento de hilo...
1.- Para un metal con una separación interatómica de 0,2nm y para el que la masa efectiva m* de los electrones coincide prácticamente con la real, calcular la anchura de la banda.
a) 3eV
b) 2,5eV
c) 1,8eV
d) 4eV
e) 1eV
1.- Para un metal con una separación interatómica de 0,2nm y para el que la masa efectiva m* de los electrones coincide prácticamente con la real, calcular la anchura de la banda.
a) 3eV
b) 2,5eV
c) 1,8eV
d) 4eV
e) 1eV
Re: Dudas estado sólido
Otra más:
1.- La energía cinética para que sea posible la difracción de neutrones a través de cristales ( distancia interatómica=1 armstrong) debe ser:
a) 1,12 eV
b) 0,95 eV
c) 0,16 eV
d) 0,0130 eV
e) 0,0825 eV
1.- La energía cinética para que sea posible la difracción de neutrones a través de cristales ( distancia interatómica=1 armstrong) debe ser:
a) 1,12 eV
b) 0,95 eV
c) 0,16 eV
d) 0,0130 eV
e) 0,0825 eV
- Usuario0410
- Rn

- Mensajes: 876
- Registrado: 23 Sep 2013, 09:48
Re: Dudas estado sólido
\(p=mv=\frac{h}{\lambda} \Rightarrow v=\frac{h}{m\lambda}\)soiyo escribió:Otra más:
1.- La energía cinética para que sea posible la difracción de neutrones a través de cristales ( distancia interatómica=1 armstrong) debe ser:
a) 1,12 eV
b) 0,95 eV
c) 0,16 eV
d) 0,0130 eV
e) 0,0825 eV
donde m es la masa de un neutrón y \lambda el armstrong, te saldrán unos 3956 m/s.
Y con la velocidad sacas la energía cinética \(\frac{1}{2}mv^2=0.082 \quad eV.\)
Re: Dudas estado sólido
Usuario0410 escribió:\(p=mv=\frac{h}{\lambda} \Rightarrow v=\frac{h}{m\lambda}\)soiyo escribió:Otra más:
1.- La energía cinética para que sea posible la difracción de neutrones a través de cristales ( distancia interatómica=1 armstrong) debe ser:
a) 1,12 eV
b) 0,95 eV
c) 0,16 eV
d) 0,0130 eV
e) 0,0825 eV
donde m es la masa de un neutrón y \lambda el armstrong, te saldrán unos 3956 m/s.
Y con la velocidad sacas la energía cinética \(\frac{1}{2}mv^2=0.082 \quad eV.\)










Gracias....sin comentarios....
Re: Dudas estado sólido
Si es dopado la concentración no sería igual, ¿No sería la 3 la correcta?28. Un material semiconductor ha sido dopado con átomos
de boro (impureza aceptadora). Si estamos a
temperatura ambiente podemos afirmar:
1. Se trata de un semiconductor intrínseco.
2. La concentración de cargas positivas será igual a la de
cargas negativas.
3. La concentración de cargas positivas será mayor a la
de cargas negativas.
4. La concentración de cargas positivas será menor a la
de cargas negativas.
5. La concentración de electrones será superior a la de
huecos.
Entiendo que si un Hamiltoniano conmuta con Lz también debería conmutar con L2, ¿No?59. Una molécula diatómica está orientada según el eje
Z. Su momento angular total es L. Considerando que
los electrones de la molécula están sometidos a un
potencial de Hartree en aproximación de un electrón
y en ausencia de perturbaciones (como por ejemplo
la rotación de la molécula) el hamiltoniano del sistema
conmuta con:
1. L2.
2. L2 y Lz.
3. L2 , Lx y Ly.
4. Lx y Ly.
5. Lz.
Yo pensaba que la masa efectiva de los huecos es negativa :S ¿Me equivoco?100. Respecto de la masa efectiva y de la carga de huecos
y electrones que contribuyen a la conducción a partir
de la teoría de bandas, se puede afirmar que:
1. Ambos tienen masa efectiva positiva y carga de
signo contrario.
2. Ambos tienen masa efectiva negativa y carga de
signo contrario.
3. Los electrones tienen masa efectiva y carga negativas,
y los huecos tienen masa efectiva y carga positivas.
4. Los electrones tienen masa efectiva positiva y carga
negativa, y los huecos masa efectiva negativa y
carga positiva.
5. Ambos tienen masa efectiva negativa y cargas del
mismo signo.
Muchas gracias
Re: Dudas estado sólido
Rey11 escribió:Si es dopado la concentración no sería igual, ¿No sería la 3 la correcta?28. Un material semiconductor ha sido dopado con átomos
de boro (impureza aceptadora). Si estamos a
temperatura ambiente podemos afirmar:
1. Se trata de un semiconductor intrínseco.
2. La concentración de cargas positivas será igual a la de
cargas negativas.
3. La concentración de cargas positivas será mayor a la
de cargas negativas.
4. La concentración de cargas positivas será menor a la
de cargas negativas.
5. La concentración de electrones será superior a la de
huecos.
Si, seria la 3
Entiendo que si un Hamiltoniano conmuta con Lz también debería conmutar con L2, ¿No?59. Una molécula diatómica está orientada según el eje
Z. Su momento angular total es L. Considerando que
los electrones de la molécula están sometidos a un
potencial de Hartree en aproximación de un electrón
y en ausencia de perturbaciones (como por ejemplo
la rotación de la molécula) el hamiltoniano del sistema
conmuta con:
1. L2.
2. L2 y Lz.
3. L2 , Lx y Ly.
4. Lx y Ly.
5. Lz.
El hamiltoniano si conmuta con L^2...yo creo que aqui la clave esta en el potencial de Hartree...te dejo un link a ver si encuentras tu la solucion porque yo ya me pierdo con la mecanica cuantica tan profunda http://sedici.unlp.edu.ar/bitstream/han ... equence=31
Yo pensaba que la masa efectiva de los huecos es negativa :S ¿Me equivoco?100. Respecto de la masa efectiva y de la carga de huecos
y electrones que contribuyen a la conducción a partir
de la teoría de bandas, se puede afirmar que:
1. Ambos tienen masa efectiva positiva y carga de
signo contrario.
2. Ambos tienen masa efectiva negativa y carga de
signo contrario.
3. Los electrones tienen masa efectiva y carga negativas,
y los huecos tienen masa efectiva y carga positivas.
4. Los electrones tienen masa efectiva positiva y carga
negativa, y los huecos masa efectiva negativa y
carga positiva.
5. Ambos tienen masa efectiva negativa y cargas del
mismo signo.
Quiza me equivoque pero creo que la masa efectiva de los electrones es positiva....es lo que recuerdo de mis examenes de electronica....
Muchas gracias