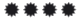En el enunciado de esta, ¿cómo puede aparecer la misma variable, la \(x\), tanto en el integrando como en el límite de integración?
Alguien me la explica.
230
Moderador: Alberto
- marcocangrejo
- Si
- Mensajes: 134
- Registrado: 19 Sep 2013, 10:33
Re: 230
¿Cómo se hace la integral? pensé en que era la función gamma, pero no. Y si la haces por partes se complica mucho...
Re: 230
Vale no, acabo de mirar como lo hice en el examen (no lo encontraba...)
Yo pasé la derivada dentro de la integral, hice:
\(\frac{d}{dx} \int_{1}^{2x} dt \frac{e^{xt}}{t} = \int_{1}^{2x} dt \frac{d(\frac{e^{xt}}{t})}{dx} = \int_{1}^{2x} dt {e^{xt}= \frac{e^{2x^2}}{x}-\frac{e^x}{x}\)
Me suena que cuando la variable que integra es diferente de la que deriva se podía hacer en el orden que quisieras que daba lo mismo...
Yo pasé la derivada dentro de la integral, hice:
\(\frac{d}{dx} \int_{1}^{2x} dt \frac{e^{xt}}{t} = \int_{1}^{2x} dt \frac{d(\frac{e^{xt}}{t})}{dx} = \int_{1}^{2x} dt {e^{xt}= \frac{e^{2x^2}}{x}-\frac{e^x}{x}\)
Me suena que cuando la variable que integra es diferente de la que deriva se podía hacer en el orden que quisieras que daba lo mismo...
- marcocangrejo
- Si
- Mensajes: 134
- Registrado: 19 Sep 2013, 10:33
Re: 230
Pero, por ejemplo, si haces esta derivada:
\(\frac{d}{dx} \int^x_0 xt dt\)
Hagamos primero la integral y luego la derivada:
\(\frac{d}{dx} \left[ x\frac{t^2}{2} \right]_0^x = \frac{d}{dx} \left( \frac{x^3}{2} \right) = \frac{3x^2}{2}\)
Si ahora lo hacemos al revés: metemos la derivada dentro de la integral y luego integras
\(\int_0^x \frac{d}{dx}\left( xt\right) dt = \int^x_0 t dt = \left[ \frac{t^2}{2} \right]_0^x = \frac{x^2}{2}\)
\(\frac{d}{dx} \int^x_0 xt dt\)
Hagamos primero la integral y luego la derivada:
\(\frac{d}{dx} \left[ x\frac{t^2}{2} \right]_0^x = \frac{d}{dx} \left( \frac{x^3}{2} \right) = \frac{3x^2}{2}\)
Si ahora lo hacemos al revés: metemos la derivada dentro de la integral y luego integras
\(\int_0^x \frac{d}{dx}\left( xt\right) dt = \int^x_0 t dt = \left[ \frac{t^2}{2} \right]_0^x = \frac{x^2}{2}\)
- marcocangrejo
- Si
- Mensajes: 134
- Registrado: 19 Sep 2013, 10:33
Re: 230
Encontré una fórmula que da la solución. Fórmula de Leibnitz:
\(\frac{d}{dx}\left( \int_{g(x)}^{h(x)} f(t,x)dt \right) = \int_{g(x)}^{h(x)} \frac{\partial f}{\partial x}dt + f(h(x))h'(x) - f(g(x))g'(x)\)
Con esta el resultado es:
\(\frac{2e^{2x^2}-e^x}{x}\)
La 1
\(\frac{d}{dx}\left( \int_{g(x)}^{h(x)} f(t,x)dt \right) = \int_{g(x)}^{h(x)} \frac{\partial f}{\partial x}dt + f(h(x))h'(x) - f(g(x))g'(x)\)
Con esta el resultado es:
\(\frac{2e^{2x^2}-e^x}{x}\)
La 1
Re: 230
Juer, pues yo esta la hice con el Teorema Fundamental del Cálculo, que viene a decir ésto

Si lo aplico para nuestra función, me queda \(\frac{e^{2x^{2}}}{x}\) porque el segundo miembro se me anula, al hacer a'(x) = 0 y ser a(x) una constante... como no me daba resultado no respondí. A ver si alguien me dice algo al respecto porque sino voy a reclamarla

Si lo aplico para nuestra función, me queda \(\frac{e^{2x^{2}}}{x}\) porque el segundo miembro se me anula, al hacer a'(x) = 0 y ser a(x) una constante... como no me daba resultado no respondí. A ver si alguien me dice algo al respecto porque sino voy a reclamarla
Re: 230
Vale debe ser que una forma aún más general de encontrarlo es con lo del Leibniz de los coj***, que la función de dentro de la integral puede depender de x y de t. Pfffffff... primera vez que lo veo oiga. A mí en cálculo I no me lo explicaron 
- marcocangrejo
- Si
- Mensajes: 134
- Registrado: 19 Sep 2013, 10:33
- Usuario0410
- Rn

- Mensajes: 876
- Registrado: 23 Sep 2013, 09:48
Re: 230
Thanks marcocangrejo, efectivamente la 1 es la correcta. Gracias